Embedding assessment into pedagogical practice
One of the reasons, I have enjoyed this text so much is the parallels of thought with my own eclectic beliefs around teaching and learning. Hattie, Fisher and Frey’s final chapter in their book, Visible learning for mathematics explores the importance of assessment, feedback and meeting the needs of all learners.
Rather than using the terminology of formative and summative assessment, the authors use formative and summative evaluation. Their argument for this choice is that as the evaluator, it is the teacher’s role to interpret where a student is during and after a lesson and how to improve his or her teaching in response to this evaluation.
Hattie, Fisher and Frey state that it is daily formative evaluation that allows to teachers to make instructional decisions about what will occur next. Carol-Anne Tomilson, the guru of differentiation states that formative assessment is the heart of differentiation as it provides the evidence as to what students know, don’t know and when done correctly, formative assessment provides both the teacher and student with information as to what to do next. The authors suggest a process for formative evaluation with the following key elements:
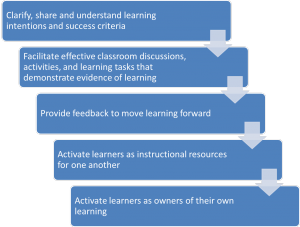
Taken from Hattie, Fisher and Frey Visible learning for mathematics
Hattie has several internal questions for learners to self-regulate and for teachers to ask about their instruction:
- Where am I going? What are my goals?
- How am I going there? What progress have I made towards the goal?
- Where to next? What activities can I do to make better progress?
Some examples of strategies to check for student understanding include: asking questions; numbered heads together; response cards; purposeful sampling; exit tickets; and lots of opportunities to self-assess.
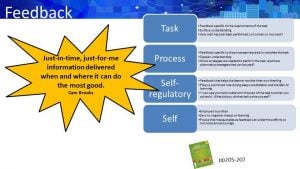
Feedback ( a slide from a maths presentation I conducted)
Hattie, Fisher and Frey discuss feedback for the teacher (adjusting teaching) and feedback for the student (adjusting learning). Hattie considers the four levels of feedback (task, process, self-regulatory and self) and considers each type’s impact. Not surprisingly the most common types of feedback are on task and process. However, for students to work towards self-regulation, self-regulatory feedback is crucial. It plays a prominent role during deep and transfer learning. The final type of feedback, self (Excellent job! You are so smart!) appears to have a zero to negative impact on learning. The effect size of feedback that fosters learning and perseverance has an effect size of 0.75.
The authors discuss the importance of differentiation in order to meet the needs of all the learners. They quote Tomilson and write that differentiated instruction is the use of a variety of instructional approaches to modify content, process, and/or products in response to the learning readiness and interest of academically diverse students (1995, p.80).
They conclude the chapter with some evidence-based provocations.
- Grade-level retention has an effect size of -0.13, yet a Response to Intervention (RTI) where students receive supplemental and intensive interventions throughout the year delivered by knowledgeable adults has an effect size of 1.07.
- Ability grouping – within-class and between-class ability group that is rigid, long-term and can make assumptions about student learning needs should be avoided (effect size of ability grouping is 0.12). Needs-based instruction with flexible grouping however can be very effective as it is student-centred, based on students’ understandings and engages students in small group learning (effect size of small group learning is 0.49).
- Test prep, including teaching test-taking skills, has insufficient evidence to justify continued use and has an effect size of 0.27. It wastes a lot of time and the gains are short-term. What does need to be taught is the content and how to learn the content (effect size for study skills is 0.63) and how to best prioritise time doing a task within the context of regular lessons. The best test prep is ongoing, high-quality instruction (p230).
- Homework generally has little impact on students’ learning and has an effect size of 0.29. This does alter as students move through their schooling years – early years – 0.10, middle school level – 0.30 and high school level – 0.55. This can be related to the type of homework given as students get older. Homework that provides another chance to rehearse something already taught and that the student has already begun to master can be effective. Homework that involves new materials, projects or work students cannot do independently is the least effective.
My own connections
This year, the Metro region of Qld State Schools has done a lot of work around what makes a standards based curriculum (such as the Australian Curriculum) work well. One of those aspects is teacher expertise that embeds assessment into pedagogical practice. When I begin planning a unit of work or the teaching of a concept, I backward map from the summative assessment task. It is important to have the end goal in mind. The best way I can really understand the demands of the task is to actually do the assessment myself and to unpack the marking guide, so I can provide opportunities for students to have unlimited growth and personal learning.
I then consider what I already know about the students in relation to the demands of the assessment and the important concepts of the unit and design a quick pre-assessment for things I don’t know. Finding out what students know and don’t know allows precision of teaching.
As the unit progresses, I then have quick formative assessments in mind, those I will do daily and those that I use as more formal check ins with my fellow year level teachers. These allow me to give students ‘just-in-time, just-for-me’ information when and where it can do the most good.
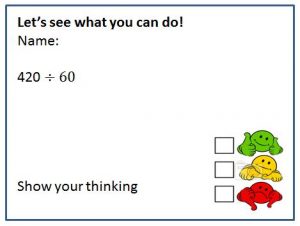
Check out ticket – mental strategies for multiplication and division
One quick formative assessment that I use consistently is the exit ticket. Not only am I able to give ‘just-in-time’ feedback to individual students, but I am able to see trends and patterns and adjust my teaching and groupings to cater for these. This particular image of one I used in a year 4/5 class gave me so much information. I could see what mental strategies students were applying, what stage of multiplicative thinking they were at, whether they could justify their thinking and a self-reflection on where they felt they were in their application of mental strategies.
This embedding of assessment (and feedback) within pedagogical practice means no surprises when the summative assessment is given. The students and I know how they are going and what their next steps for learning is. I am also able to adjust my teaching in response to real-time data and make good decisions about instruction. The brilliant thing is that the data gathered in the summative assessment can then be used to inform the next unit.
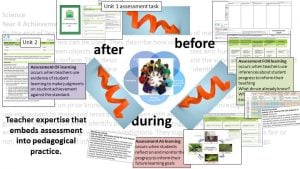
Embedding assessment in pedagogical practice
Where are you when it comes to assessment, feedback and meeting the needs of your learners particularly in the learning area of mathematics? This final chapter explores these ideas in detail. Hattie, Fisher and Frey have produced a fabulous book that is easy to read, easy to apply, makes learning visible and puts the student at the centre of teaching and learning. Well worth a read.

