What were your mathematics lessons like as a student? What would students say about your current mathematics lessons?
In primary school, I can remember the blackboard (yes, I am that old) being covered in numerous columns of mathematical operations, all very similar but with increasing difficulty.  I don’t remember receiving too many problems to solve and I certainly wasn’t allowed to discuss my solutions or ways of working. In fact, there really was only one way to do it – the traditional algorithm as modelled by the teacher – on my own and in silence.
I don’t remember receiving too many problems to solve and I certainly wasn’t allowed to discuss my solutions or ways of working. In fact, there really was only one way to do it – the traditional algorithm as modelled by the teacher – on my own and in silence.
In the beginning of my teaching career, I emulated some of what I experienced in my own education – lots of operations for students to solve. I made it harder by setting them out horizontally or increasing the size of the numbers. Problem solving was on a Friday. If students finished quickly, I gave them more. Thankfully, my understanding of higher order thinking, collaboration, discussion, and the importance of problem solving and reasoning increased as my experience as a classroom teacher increased.
Imagine my concern last year, when during another heated discussion over homework, my son in year 10 argued, ‘Why do I have to do twenty of these, Mum, when I have already got the first three right? They are all the same?” I had no answer as he was absolutely right. Completing extensive, repeated, context-free exercises is not going to develop the transferable and flexible understanding of mathematical processes (Hattie, Fisher and Frey, 2017).
Procedural fluency cannot be developed without true and meaningful comprehension and ‘drill-and-kill’ exercises without understanding can harm students’ mathematical understandings, their motivation level, and the way they view mathematics. (Hattie, Fisher and Frey, 2017, p75)

Mathematical tasks and talk that guide learning is the title for Chapter 3 in the text, Visible learning for mathematics.
When it comes to planning and implementing maths lessons, Hattie, Fisher and Frey (2017) mention three important ideas to take into consideration.
1. Spaced practice is more effective than mass practice with an effect size of 0.71.
2. Math is not a speed race and speed is not a part of fluency. Speed can damage students’ self-perception of their maths ability.
3. Tasks should not focus solely on procedures as conceptual understanding can be sacrificed.
Good mathematical instruction involves reasoning, exploration, flexible thinking and making connections. Students should know that learning isn’t easy and that there is an enjoyment in meeting the challenges of learning demands.
There are typically two types of tasks – exercises and problems. Exercises make up most of traditional text book practice, are without context and are provided to allow students to practise a particular skill. Problems are generally written in words and apply or provide a context for a mathematical concept. There are those that focus on using a particular concept and those that are non-routine or open ended.
Problems should be used to introduce an idea so that students can model a situation and begin to develop conceptual understanding. Non-routine or open ended problems involve more that applying a mathematical procedure for solutions. Students need a toolkit of strategies and some ‘out-of-the-box’ thinking to solve these.
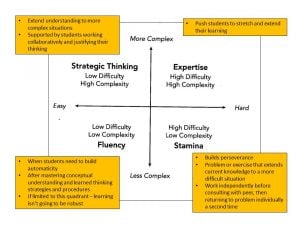
Hattie, Fisher and Frey, 2017, p77
Hattie, Fisher and Frey advise teachers to consider the level and type of challenge a given task provides and have developed a fluency quadrant to assist with this consideration:
Low Difficulty Low Complexity
- When students need to build automaticity
- After mastering conceptual understanding and learned thinking strategies and procedures
- If limited to this quadrant – learning isn’t going to be robust
High Difficulty Low Complexity
- Builds perseverance
- Problems or exercises that extend current knowledge to a more difficult situation
- Students work independently before consulting with a peer, then returning to problem individually a second time
Low Difficulty High Complexity
- Extends understanding to more complex situations
- Supported by students working collaboratively and justifying their thinking
High Difficulty High Complexity
- Pushes students to stretch and extend their learning
Hattie, Fisher and Frey (2017) mention a number of characteristics that assist students to build understanding and confidence in mathematics. These include:
- Teachers using questioning and prompts to build understanding.
- Mistakes being valued and seen as opportunities.
- Students considering different approaches and noting their similarities and differences.
- Lessons having an element of productive struggle which is accompanied by perseverance.
- Rich discourse.

The chapter finishes with a focus on posing purposeful questions and the use of prompts and cues. Purposeful questions help teachers check for understanding and the use of prompts and cues encourages students to do the cognitive work, moving them on in their learning.
Identifying the right approach at the right time is critical. Misalignment between tasks and types of learning (surface, deep and transfer) puts students at risk.
Giving students appropriate tasks at the right time in their learning cycle is crucial to move students from surface to deep and transfer learning (Hattie, Fisher and Frey, 2017, p73).
My next blog will explore what tasks the authors have found to work at each stage of the learning.

