Too often, learning ends at the surface level. (Hattie, Fisher and Frey, 2017, p131) How do we go beyond surface learning and into deeper learning?
As mentioned in my previous blog, surface learning is the beginning of conceptual understanding. The challenge for teachers is not to over rely on it and to know when and how to move students from surface to deep learning.  Deep learning (the focus of Hattie, Fisher and Frey’s fifth chapter in their text Visible learning form mathematics) provides students with opportunities to consolidate mathematical understandings and to make deeper connections among ideas.
Deep learning (the focus of Hattie, Fisher and Frey’s fifth chapter in their text Visible learning form mathematics) provides students with opportunities to consolidate mathematical understandings and to make deeper connections among ideas.
One of the reasons I write this blog is to take my own reading to a deeper level and to make connections with other research and focuses in my work.
With appropriate instruction, surface learning transforms into deep learning. (Hattie, Fisher and Frey, 2017, p35)
In deep learning, mathematical tasks will be cognitively more demanding, more open-ended and have multiple ways of solving them or multiple solutions. As teachers, we have to make judgments about how much surface learning is required in preparation for this deep learning.
Who is doing the talking?
To promote deep learning, students need opportunities for mathematical talk.  Accountable talk is promoted by Lyn Sharratt in her work in the Metropolitan region. Hattie, Fisher and Frey state that students should be drenched in accountable talk and this chapter provides a number of language frames that scaffold the use of language to support a mathematic topic. A number of other supports for accountable talk are also mentioned.
Accountable talk is promoted by Lyn Sharratt in her work in the Metropolitan region. Hattie, Fisher and Frey state that students should be drenched in accountable talk and this chapter provides a number of language frames that scaffold the use of language to support a mathematic topic. A number of other supports for accountable talk are also mentioned.
Who is doing the thinking?
 When it comes to mathematical thinking in whole class or group discussion, the authors mention three sociomathematical norms, norms that promote true mathematical discourse. Reading the text gives an insight into how a skilled mathematics teacher can promote the following:
When it comes to mathematical thinking in whole class or group discussion, the authors mention three sociomathematical norms, norms that promote true mathematical discourse. Reading the text gives an insight into how a skilled mathematics teacher can promote the following:
- Explanations that are mathematical arguments and include justifications.
- Errors as opportunities to reconsider problems from a different point of view.
- Intellectual autonomy that recognises participation.
Are students being encouraged to collaborate?
Collaboration is another important dimension of deep learning. Humans learn better when they interact with other humans and the authors recommend that 50% of class time over a week be devoted to student discourse and interaction with their peers. Effective collaboration and cooperative learning tasks must:
- be complex enough that students need to work together.
- allow for argumentation.
- include sufficient language support.
- provide individual and group accountability.
How are students being grouped?
Students should be grouped strategically. The authors point out that fixed ability grouping does not help students to understand the math they are learning. It can affect motivation and make students dislike maths. The most effective grouping strategy is one that is flexible and balanced and allows for a moderate range of skills.
Are you using manipulatives and encouraging multiple representations?
Just as in the surface learning chapter, this one wraps up with a look at the importance of multiple representations and the strategic use of manipulatives to promote deep learning. Students demonstrate stronger problem-solving abilities and deeper mathematical understanding when are encouraged to represent mathematics in a variety of ways. Representations can be physical, visual, symbolic, verbal and contextual.
In the Metropolitan region of Queensland, my colleagues and I have always promoted the think board (an idea we found in First Steps in Mathematics), It can be used in a variety of ways as a graphic organiser for different representations and a way of showing the connections.
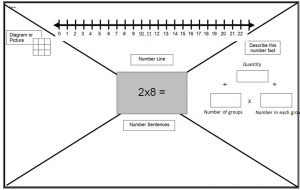
The thinkboard can be used as pre-assessment, formative assessment or collaborative learning

An example of an annotated think board
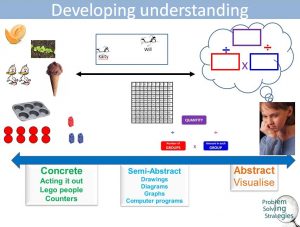
Using the CSA model to develop use of the Multiplication and Division Triangle (a strategy for problem solving)
Manipulatives shouldn’t be limited to surface learning and can be used to make concepts concrete and visible. They assist students to see patterns, make connections and form generalisations. Again the Concrete Semi abstract Abstract (CSA) model (also promoted by my Metropolitan colleagues) is a useful frame to assist teachers with choices around the instructional sequence from physical to visual to symbolic representations.
All of the above have high effect sizes and assist in making deep learning visible. My next blog will look at transfer learning, the application of surface and deep learning.

