 The true purpose of getting an education is to apprentice students into becoming their own teachers. We want them to be self-directed, lifelong learners , and to have curiosity about the world. We want them to have the tools they need to formulate their own questions, pursue meaningful answers, and through metacognition, be aware of their own learning in the process. (Hattie, Fisher and Frey, 2017, p176)
The true purpose of getting an education is to apprentice students into becoming their own teachers. We want them to be self-directed, lifelong learners , and to have curiosity about the world. We want them to have the tools they need to formulate their own questions, pursue meaningful answers, and through metacognition, be aware of their own learning in the process. (Hattie, Fisher and Frey, 2017, p176)
Hattie, Fisher and Frey mention three phases of learning – surface, deep and transfer. My previous two blogs explored the first two phases of learning: surface and deep. The final phase is that of transfer. In mathematics, this phase occurs when students are able to make connections among mathematical understandings and then use those understandings to solve problems in unfamiliar situations, while being very aware of what they are doing. Because learning is cyclical, transfer occurs all the time.
The authors use the example of Linda who understood the mechanics of mathematics (surface learning mixed with a little bit of deep learning) but had no idea how to apply that knowledge to real world contexts.
Why do I need this?
Linda reminds me very much of myself when I attended secondary school and continually battled with the subject of maths. I loved it, particularly the challenge of the discipline but was extremely frustrated in that I did not know how to apply what I had learned to different situations or real world contexts. I also constantly questioned why I had to learn certain things, such as sine, cos and tan. I was never shown how trigonometry is used in contexts outside of school. Relevancy is a major condition of transfer which is basically answering the questions, “Why do I need to learn this and when will I ever use it?”
Learning becomes more meaningful when learners see what they’re learning as being more meaningful in their own lives.
Hattie, Fisher and Frey state that it is also extremely important that teacher knows the learner developmentally and experientially in order to promote transfer of learning. The authors recommend two stages of transfer: near and far. Near transfer occurs when a new situation is paired to a context that a student has already experienced. A great way for students to develop transfer learning is to consider similarities and differences between the new and a recently completed idea.
Venn diagram
Using graphic organisers such as the Venn diagram can help students consider the similarities and differences.Hattie writes that comparing and contrasting new with old problems has an effect size of 1.23.
The leap is bigger for far transfer as the student has to make connections to more removed situations.
Hattie, Fisher and Frey mention a few things to consider when planning tasks for transfer. Tasks:
- should be selected to encourage connections
- should be of higher complexity with higher difficulty
- may not have clear entry points
- may have multiple steps
- may not have one correct solution – students have to make judgments about the best solution and justify their thinking with evidence
- incorporate maths ideas that can be applied in other learning areas
- may take more than one lesson to solve
- should have relevancy
- should be developmentally appropriate.
Metacognition, the ability to think about our thinking, promotes transfer learning. Palinscar (2013) described metacognitive awareness as having three parts:
- knowledge about our learning selves
- an understanding of the task demands and necessary strategies to complete it
- the means to monitor learning and self-regulate
To develop metacognitive skills, students need to learn the art of self-questioning. Self-verbalisation and self-questioning have an effect size of 0.64. Self-questioning enables students to track their understanding and re-align when off target. Hattie recommends using pre-lesson questions (What are today’s goals?) and post-lesson questions (What was today’s goals?) to encourage metacognition.
Self-reflection is a follow-up technique after the lesson that encourages students to understand where they were and where they are now.

Self-reflection
Rich class discussion promotes transfer learning. In mathematical discussions, students should be able to represent their thinking to others, pose questions, and engage in disagreements respectfully. The caveat is that it is not unrelated storytelling, random opinion sharing or teachers doing most of the talking. The teacher’s role is to use questioning to lift student thinking, press for evidence and have students make links amongst concepts.
The caveat is that it is not unrelated storytelling, random opinion sharing or teachers doing most of the talking. The teacher’s role is to use questioning to lift student thinking, press for evidence and have students make links amongst concepts.
For students to take the driver’s seat of their own learning, they need a sense of how the mathematics that they know is organised. Creating an organisational structure for mathematical knowledge is a powerful tool.
Peer tutoring requires the tutor to connect what the tutee needs to learn to what the tutee already knows and understands. Peer tutoring has an effect size of 0.55 and works best when programs are structured, the tutor receive training and the tutor and tutee are of different ages. It allows the tutor to solidify his/her understanding and the tutee to improve their learning.
Giving students opportunities to explore their own ways of using what they have learned is critical for transfer learning and should be woven into classroom life. Students should be continually challenged to develop projects and investigations across the school day.
This makes me think of a recent initiative being used in Queensland: Age Appropriate Pedagogies which encourages the use of a range and balance of pedagogical approaches in the classroom.

Age appropriate pedagogies conceptual framework
The conceptual framework includes six approaches to teaching and learning: event-based, project, explicit instruction, inquiry learning, play-based learning, direct teaching/instruction and a blended approach (Department of education and training, Qld Government). Only ever using one approach such as direct instruction will limit a student’s ability to transfer learning.
Problem-solving teaching also encourages the transfer of mathematics learning and is different to a problem-solving process.

Problem-solving teaching in mathematics
It is similar to the design thinking necessary for the new Australian Curriculum learning area of Technologies.
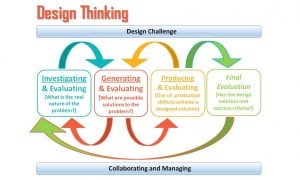
Design thinking in AC Technologies – thanks to Grant Smith (one of my regional colleagues)
Problem-solving teaching helps students engage in the process of determining the cause of a problem; using multiple perspectives to uncover issues; identifying, prioritising, and selecting alternatives for a solution; designing an intervention plan; and evaluating the outcomes. (Hattie, Fisher and Frey, 2017, p193)
Design challenges for any age group can be identified by listening to students’ wonderings about the world around them. An example may be designing a school garden to grow vegetables for cooking.

How to design a school garden?
Reciprocal teaching also assists students to transform their mathematical thinking and is a literacy strategy that develops comprehension of the mathematical problem. Students work collaboratively to build their understanding of texts. There are four stages and students are encouraged to keep a record of their thinking and work. :
- predicting – students use knowledge of mathematics and the information provided to predict what is happening and to decide what mathematics may be needed to solve the problem.
- clarifying – students make lists of information that they might need to solve the problem – unfamiliar vocabulary, known facts and necessary information to solve the problem.
- solving – students use their problem-solving strategies to find one or more solutions to the problem and are encouraged to use multiple representations.
- summarising – this is a time for individual self-reflection that includes justifying the solution, reflecting on the effectiveness of the selected strategies and evaluating their participation.
Students need the opportunity to apply what they have learned in mathematics to unfamiliar situations but it would be nearly impossible to transfer without surface and deep learning. Transfer learning should not be left to chance and requires caring teachers to deliberately design opportunities by knowing their students and using effective strategies.
Stay tuned. My blogs have slowed down as I am back at work but I have one more blog for this text. It will look at the last chapter – Assessment, feedback and meeting the needs of all learners and will be posted within the next couple of weeks.

